几何问题是行测数量关系中的必考考点，它的考察包括平面几何和立体几何，其中平面几何的考察以求解长度和面积为主，立体几何主要考察的是体积和表面积的求解，而在立体几何的考察中还有一种比较有意思的题型就是立体几何染色问题。对这类问题有了解过的朋友都知道，它对于我们的空间思维能力要求比较高，那么空间思维能力较差的话，我们要怎样应对这类题目呢?接下来跟大家一起来探讨一下，相信只要我们掌握了相应的基础知识，这类问题解决起来就会游刃有余了。

　　一、立体几何染色问题的基础知识

　　在一个边长为n的正方体表面全部涂上蓝色，将其切成边长为1的小正方体，则在这些小正方体可分为3面有色、2面有色、1面有色和0面有色四种。从下图上我们看出一个正方体有8个顶点，12条棱，6个面，其中顶点上的8个小正方体3面都涂上了蓝色，在棱上而不在顶点上的小立方体2面涂上了蓝色，正方体的外表面非棱非角部分面涂了蓝色。故：

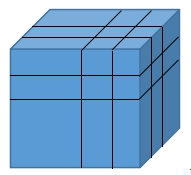
　　3面有色的一共有：8个;

　　2面有色的一共有：12×(n-2)个;

　　1面有色的一共有：6×(n-2)2个;

　　0面有色的一共有：(n-2)3个。

　　同理，我们可以拓展到长方体。在一个长、宽、高分别为a、b、c的长方体表面全部涂上颜色，将其切成边长为1的小正方体，则在这些小正方体可分为3面有色、2面有色、1面有色和0面有色四种，其中：

　　3面有色的一共有：8个;

　　2面有色的一共有：4×{(a-2)+(b-2)+(c-2)}个;

　　1面有色的一共有：2×{(a-2)×(b-2)+(a-2)×(c-2)+(b-2)×(c-2)}个;

　　0面有色的一共有：(a-2)×(b-2)×(c-2)个。

　　二、试题应用

　　1、一个边长为8cm的立方体，表面涂满油漆，现在将它切割成边长为0.5cm的小立方体，问两个表面有油漆的小立方体有多少个?

　　A、144 B、168 C、192 D、256

　　【解析】两个表面被涂油漆的小立方体在棱上而不在顶点上。大立方体棱长为8cm，切成小立方体棱长为0.5cm，则每条棱被分成16段，其中两端不符合要求，因此每条棱上有14个小立方体符合。立方体共有12条棱，则符合要求的小立方体有14×12=168个。故正确答案为B。

　　2、将一个8厘米×8厘米×1厘米的白色长方体木块的外表面涂上黑色颜料，然后将其切成64个棱长1厘米的小正方体，再用这些小正方体堆成棱长4厘米的大正方体，且使黑色的面向外露的面积要尽量大，问大正方体的表面上有多少平方厘米是黑色的( )。

　　A、84 B、88 C、92 D、96

　　【解析】由长方体木块切得的小正方体中，4面黑的只有4块，2面黑的正方体有24块，而大正方体2面黑的刚好需要24块，用完，3面黑的需要8块，现在只有4块，少了4，则只能用1面黑的代替，所以每个都少了2个面，共4个，则少8个面，少了8平方厘米，故大正方体表面黑色的面积为：4×4×6-8=88。故正确答案选B。

　　3、一个5×5×5的立方体表面全部涂上红色，再将其分割成1×1×1的小立方体，取出全部至少有一个面是红色的小立方体，组成表面全部是红色的长方体，可组成的长方体的体积最大是：

　　A、125 B、98 C、96 D、94

　　【解析】至少有一个面是红色的小立方体一共有：53-(5-2)3=125-27=98个，8个3面涂色的在长方体8个顶点处，(5-2)×12=36个2面涂色的在长方体的12条棱上，一面涂色的98-8-36=54个只能放在面的中间和里面。当新长方体体积为98时，其长、宽、高分别为7、2、7(98=2×7×7)，2面涂色的需要(7-2)×8=40个，40>35，不满足，故排除B;当新长方体体积为96时，其长、宽、高分别为6、4、4(96=4×4×6)，2面涂色的需要(4-2)×8+(6-2)×4=32个，32<35，满足要求，所以可组成的长方体的体积最大是96。故正确答案选C。

　　通过以上三道题目，相信大家对于立体几何染色问题已经有了进一步的认识和理解，希望大家能够熟练掌握立体几何染色问题的基础知识，在做题的时候能够灵活运用。