在对行测数量关系的考察中,经常会有一些涉及到平均数的问题。在数学中,有4中较为常见的平均数:算数平均数、几何平均数、调和平均数、平方平均数。其中,算数平均数和几何平均数较为简单,考生也较为熟悉,平方平均数很少涉及,不是我们关注的重点,而调和平均数在试题中经常出现,有大量考题与之有关,但考生对其关注却很少。所谓调和平均数,是指![]() ,本质在于
,本质在于![]() 构成等差数列。使用调和平均数的题目一般有以下三类:等距离平均速度问题、等溶质增减溶剂问题、等发车前后过车问题等。
构成等差数列。使用调和平均数的题目一般有以下三类:等距离平均速度问题、等溶质增减溶剂问题、等发车前后过车问题等。
一、等距离平均速度问题
例1、一个人骑自行车过桥,上桥的速度为每小时12公里,下桥的速度为每小时24公里。上下桥所经过的路程相等,中间没有停顿。问此人过桥的平均速度是多少?( )(2007年天津公务员考试行测试卷第74题)
A、14公里/小时 B、16公里/小时 C、18公里/小时 D、20公里/小时
答案:B 解析:假设上桥路程为s,这道题所求的是过桥的平均速度,而结合行程问题基本公式v=S/t,可知,
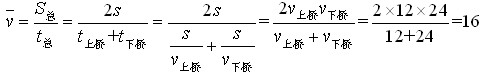
事实上,等距离平均速度有一个核心公式:![]()
(v1、v2分别代表往、返的速度),遇到类似问题只需直接带入公式即可。
二、等溶质增减溶剂问题
例2、一种溶液,蒸发掉一定量的水后,溶液的浓度为10%;再蒸发掉同样多的水后,溶液的浓度变为12%;第三次蒸发掉同样多的水后,溶液的浓度将变为多少?( )(2009年国家公务员考试行测试卷第113题)
A、14% B、17% C、16% D、15%
答案:D 解析:设第一次蒸发掉水后的溶液量为x,蒸发掉的水为y,则溶质的量为0.1x,第二次蒸发后浓度为0.1x/(x-y)=0.12,化简可得x=6y,第三次蒸发后的浓度为0.1x/(x-2y)=0.6y/4y=0.15。即第三次蒸发后,浓度变为15%。
等溶质增减溶剂也可以运用一个核心公式:
![]()
,(其中r1、r2、r3代表连续变化的浓度)。这道题目只需直接带入:
![]()
三、等发车前后过车问题
例3、某人沿电车线路匀速行走,每15分钟有一辆电车从后面追上,每10分钟有一辆电车迎面开来.假设两个起点站的发车间隔是相同的,求这个发车间隔。( )
A、11分钟 B、14分钟 C、13分钟 D、12分钟
答案:D 解析:设每隔t1分钟就遇到迎面开来的一辆电车,每隔t2分钟就有一辆车从后面超过,则有方程组
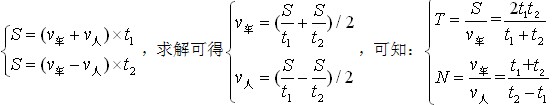
(S表示发车间距,T为发车间隔时间,v车为车速,v人为人速,N为车速和人速的比。求得
![]()
事实上,只需要掌握等发车前后过车核心公式:发车时间间隔
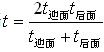
,代入题中条件可得正确答案。
调和平均数在数量关系的考试中运用非常广泛,了解并掌握“调和平均数”解题的方法,熟记调和平均数公式
![]()
,可以使得很多题目得到迅速、高效的解答。









