行测中常见的概率题型及解题技巧

　　一、P(A)=A包含的基本事件个数÷总的基本事件个数

　　例1、有10件产品，8件正品，2件次品，从这些产品中任取2件，则两件都是正品的概率是多少?

　　A、28/45 B、4/5 C、25/36 D、5/8

　　解析：设A={任取2件都是正品}，

　　二、某条件的成立的概率=1-该条件不成立的概率

　　总体概率=满足条件的各种情况概率之和;

　　分步概率=满足条件的每个步骤概率之积。

　　例2、乒乓球比赛的规则是五局三胜制。甲、乙两球员的胜率分别是60%与40%。在一次比赛中，若甲先连胜了前两局，则甲最后获胜的胜率( )

　　A、为60% B、在81%.～85%之间

　　C、在86%～90%之间 D、在91%以上

　　解析：甲获胜的概率=1-乙获胜的概率;而乙获胜等价于乙后三场都要获胜，根据分步概率的公式可知乙获胜的概率为40%×40%×40%=6.4%，因此甲获胜的概率就是93.6%，选D。

　　三、会面问题

　　例3、甲乙两人相约见面，并约定第一人到达后，等15分钟不见第二人来就可以离去。假设他们都在10点至10点半的任一时间来到见面地点，则两人能见面的概率有多大?( )(2010年4月25日多省公务员联合考试第10题)

　　A. 37.5% B. 50% C. 62.5% D. 75%

　　例4、甲、乙两人相约在 0 到 T 这段时间内, 在预定地点会面. 先到的人等候另一个人, 经过时间 t( t<T ) 后离去.设每人在0 到T 这段时间内各时刻到达该地是等可能的 , 且两人到达的时刻互不牵连.求甲、乙两人能会面的概率（ ）

　　解析：从0点开始计时，设两人到达的时刻分别为x，y，则

　　G={(x，y)︱0≤x≤T，0≤y≤T}

　　假定两人到达时刻是随机的，则问题归结为几何概型，设A表示"两人能会面"事件，则

　　G1={(x，y)︱0≤x≤T，0≤y≤T，︱x-y︱≤t} (图中的阴影部分)，

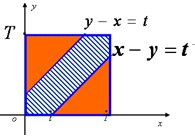
　　则：

　　注：上述题目，只需将数据应用到这个公式里，答案选D。

　　四、数学期望--随机变量的平均值

　　平均值等于各种情况与相应概率的乘积之和。

　　例5、某工厂规定:工人只要生产出一件甲级产品发奖金50元，生产出一件乙级产品发奖金30元，若生产出一件次品则扣奖金20元，某工人生产甲级品的概率为0.6,乙级品的概率为0.3，次品的概率为0.1，则此人生产一件产品的平均奖金为多少元?( )

　　A、32 B、45 C、37 D、26

　　解析：平均值=50×0.6+30×0.3-20×0.1=37，选C。